weraebooks.blogg.se

We employ the finite difference method and the orthogonal collocation method on finite elements (in two regions) and compare them. In this case, we ignore the term in the differential equation with (1/r), and think of r as x. The boundary conditions for flow between flat plates are The boundary conditions for annular flow are The boundary conditions are pipe flow are Thus, we pose the following problems (sketched in Figure 2) Here we want to see how to solve the problem numerically, including more complicated cases in which the fluids are non-Newtonian (the viscosity then depends on shear rate), or the flow is in a pipe or annulus. While the representation is messy, it is straightforward.

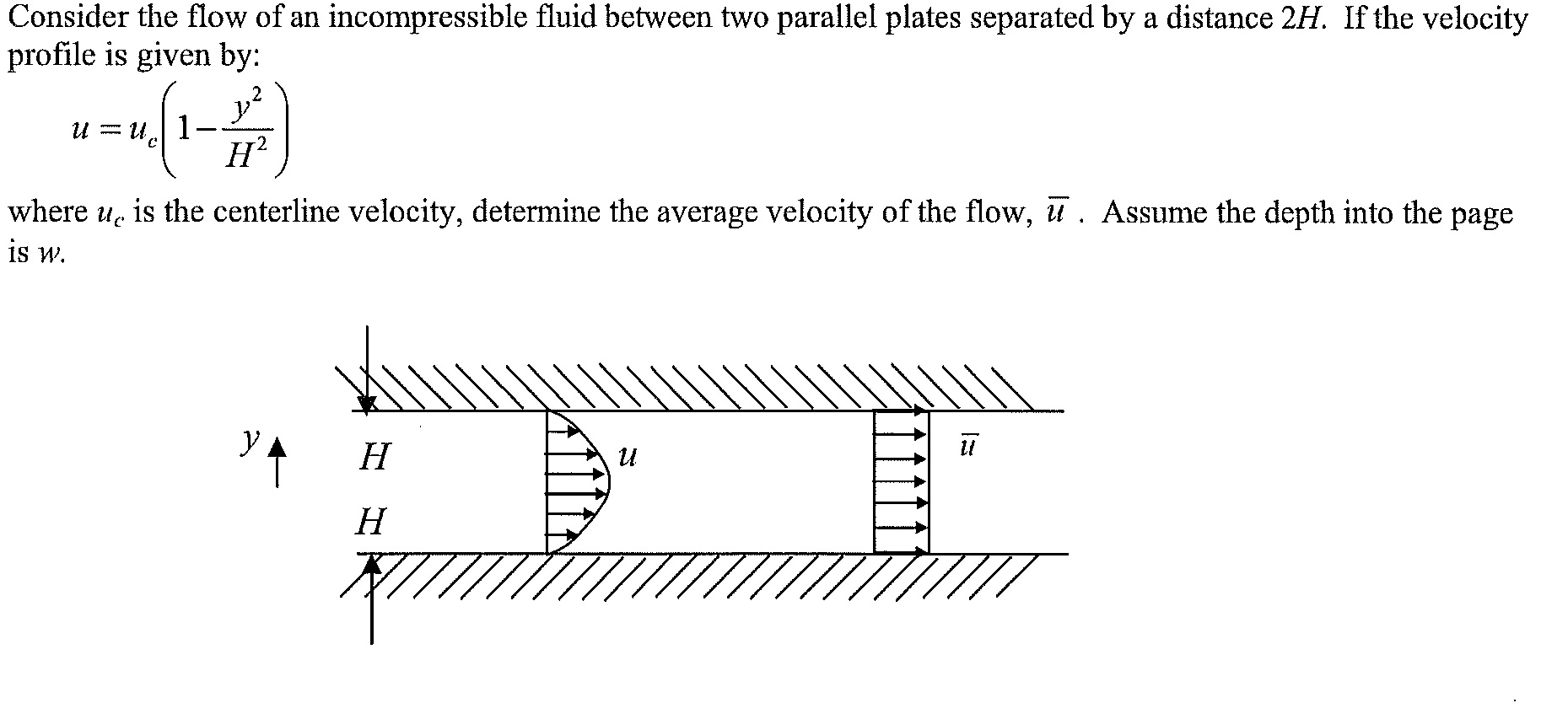
Since the right-hand side of the differential equation is a constant, the velocity is a quadratic function of position in both regions, and the constants are adjusted to satisfy the differential equation (giving the constant in front of the x 2 term) and the boundary conditions. This problem has an analytical solution (ref). We require that the velocity be continuous and that the shear stres be continuous (otherwise there would be generation of momentum at the interface). There must also be compatibility conditions at the interface between the two fluids. The boundary conditions on the solid walls are that the velocity is zero. The differential equations coming from the momentum balance are For simplicity in this first example, take both fluids as Newtonian with a constant viscosity, which is different for the two fluids. If the flow is to be fully developed, then the pressure drop per length has to be the same in both fluids otherwise there would be a transverse pressure gradient, which would lead to transverse flow, contrary to the fully developed assumption. One must solve for the location of the interface between the two fluids as well as for the velocity profile.

Flow of two immiscible fluids between flat platesĬonsider the flow of two immiscible fluids between two flat plates in fully developed flow, as shown in Figure 1. Fluid flow of one or two fluids in pipes, annuli, and between flat plates.įigure 1.